22. Parametric Surfaces and Surface Integrals
e. Vector Surface Integrals
A vector surface integral is defined as \[ \iint_S \vec{F}\cdot\,d\vec{S} =\iint_S \vec{F}(\vec R(u,v))\cdot\vec{N}\,du\,dv \] However, there is one more fine point we need to discuss before computing this type of integral.
2. Orientations
The integral must be independent of the choice of parametrization. Unfortunately, if we do something as simple as reverse the order of the parameters, i.e. \(u\) and \(v\) are interchanged, then the parametrization becomes \(\vec R(v,u)\), the tangent vectors \(\vec e_u\) and \(\vec e_v\) are interchanged and the normal is now \(\vec N=\vec e_v\times\vec e_u\) which is the negative of what it was. So the dot product \(\vec{F}(\vec R(v,u))\cdot\vec{N}\) reverses sign and the integral changes sign. To correct this ambiguity, we need to understand the orientation of the surface. A surface is orientable if it has two sides. For example, the surface of a cylinder has an inside and an outside; a horizontal plane has a top and a bottom. However a Mobius strip has only one side; so it is not orientable. For a non-orientable surface, one can compute scalar surface integrals but not vector surface integrals.
mj
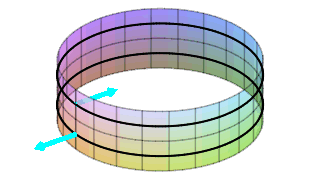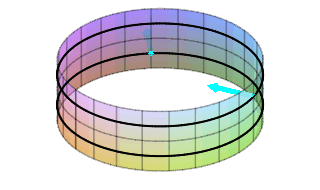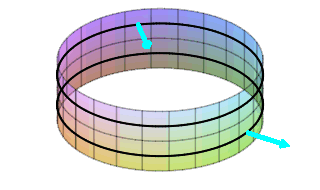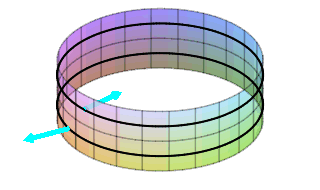
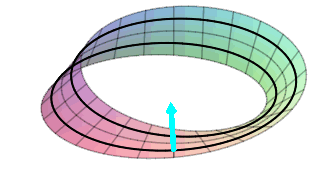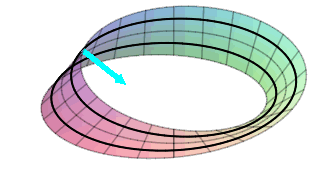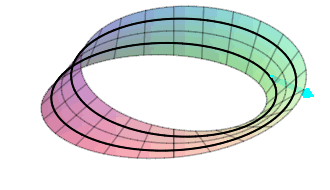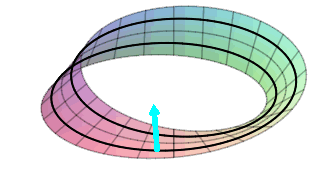
On the cylinder, there is a normal rotating around near the top pointing inward which comes around and is still pointing inward. In addition, there is a normal rotating around near the bottom pointing outward which comes around and is still pointing outward. There is no way to continuously slide the normal from the outside to the inside. There are two sides to this surface. It is orientable!
On the Mobius strip, there is a normal rotating around the strip starting pointing outward, but when it comes around, it is pointing inward, and when it comes around again, it is pointing outward again. This means that the “inward” and “outward” sides of the surface are really only one side, not two. It is non-orientable!
An orientation of an orientable surface is a specification of which side of the surface is considered to be the front of the surface. A parametrization \(\vec R(u,v)\) of a surface is oriented if the normal vector \(\vec N=\vec e_u\times\vec e_v\) points toward the front of the surface. From now on, when we want to compute a vector surface integral, we need to specify the orientation of the surface and use an oriented parametrization.
In practice, we don't worry about the orientation when we pick the parametrization. If we end up with the normal pointing toward the wrong side of the surface, then we simply reverse the sign of the normal and proceed. We will see this in the example and exercise below.
Orientations of Line Integrals
Line integrals also need to be oriented. The vector line integral \[ \int_A^B \vec F\cdot d\vec s=\int_A^B \vec F\cdot \vec v\,dt \] is understood to be oriented from \(A\) to \(B\). If we reverse the direction, then the integral will change signs: \[ \int_B^A \vec F\cdot d\vec s=-\int_A^B \vec F\cdot d\vec s \] The path is usually parametrized by a curve \(\vec r(t)\) for which \(t\) increases from \(A\) to \(B\), and hence its tangent vector \(\vec v\) points from \(A\) towards \(B\). However, if we (accidentally) parametrize it with \(t\) increasing from \(B\) to \(A\), and notice that the tangent vector points backwards, we don't need to go back and reparametrize it, we just reverse the sign of the tangent and proceed. We will see examples of this in the next part of the course on the multivariable calculus Theorems.
The importance of the orientation of a surface becomes clear when we discuss the flux of a vector field through the surface. If \(\vec{V}\) is the velocity field of a fluid then the flux of \(\vec{V}\) through a surface \(S\) is the integral \(\displaystyle \iint_S \vec{V}\cdot\,d\vec{S}\) which measures the amount of fluid which flows through the surface per unit time. If the fluid flows in the direction of the normal, then the flux is positive. If the fluid flows opposite to the normal, then the flux is negative.
Similarly, the orientation of a curve became important when we discussed the circulation of a vector field around a closed curve. If \(\vec{V}\) is the velocity field of a fluid then the circulation of \(\vec{V}\) around a curve \(C\) is the integral \(\displaystyle \int_C \vec{V}\cdot\,d\vec{s}\) which measures the amount of fluid which flows around the curve per unit time. If the fluid flows in the direction of the tangent vector, then the circulation is positive. If it flows opposite to the tangent, then the circulation is negative.
Summary: Vector Surface Integrals
- Parametrize the surface, \(\vec R(u,v)\).
- Evaluate the vector field, \(\vec F\), on the surface to get \(\vec{F}(\vec R(u,v))\).
- Find the tangent vectors and normal vector \(\vec{N}\), for the surface.
- Verify the normal is oriented properly. If necessary, reverse it.
- Compute the dot product, \(\vec{F}(\vec R(u,v))\cdot\vec{N}\).
- Evaluate the integral \(\displaystyle \iint_S \vec{F}\cdot\,d\vec{S} =\iint_S \vec{F}(\vec R(u,v))\cdot\vec{N}\,du\,dv\).
There is no Jacobian involved anywhere in the calculation. In these integrals, \(\vec{N}\) contains terms that serve the same function as a Jacobian. Often, the parameters one uses to parametrize a surface are similar or even identical to those used for cylindrical coordinates (e.g. two of \(r\), \(\theta\) or \(z\)) or spherical coordinates (e.g. two of \(\rho\), \(\phi\) or \(\theta\)). It is important to remember that these are parameters for the surface, and we are not actually integrating in cylindrical or spherical coordinates. There is no extra \(r\) or \(\rho^2\sin\phi\).
Compute \(\displaystyle \iint_P \vec{F}\cdot\,d\vec{S}\) where
\(\vec{F}=\left\langle xz,yz,z^2\right\rangle\) and the surface is the
polar cap (\(0 \le \phi \le \dfrac{\pi}{6}\)) of a sphere of radius \(2\)
with the orientation outward from the sphere.
The parametrization and normal were computed in a
previous example, but we will redo it here.
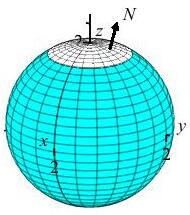
The surface is given by the parametrization:
\[
\vec R(\theta,\phi)
=\left\langle 2\sin\phi\cos\theta,2\sin\phi\sin\theta,2\cos\phi\right\rangle
\]
(Note: we have chosen the order of the parameters as \((\theta,\phi)\) to
emphasize a point later.) First, we evaluate the vector field,
\(\vec{F}=\left\langle xz,yz,z^2\right\rangle\), on the surface:
\[
\vec{F}(\vec R(\theta,\phi))
=\left\langle 4\sin\phi\cos\phi\cos\theta,4\sin\phi\cos\phi\sin\theta,
4\cos^2\phi\right\rangle
\]
Next, we find the normal vector:
\[\begin{aligned}
\vec{N}=\vec{e}_\theta\times\vec{e}_\phi
&=\left|
\begin{array}{ccc}
\hat{\imath} & \hat{\jmath} & \hat{k} \\
-2\sin\phi\sin\theta & 2\sin\phi\cos\theta & 0 \\
2\cos\phi\cos\theta & 2\cos\phi\sin\theta & -2\sin\phi
\end{array}
\right| \\
&=\hat{\imath}(-4\sin^2\phi\cos\theta)
-\hat{\jmath}(4\sin^2\phi\sin\theta) \\
&\quad+\hat{k}(-4\sin\phi\cos\phi\sin^2\theta-4\sin\phi\cos\phi\cos^2\theta) \\
&=\left\langle -4\sin^2\phi\cos\theta,-4\sin^2\phi\sin\theta,
-4\sin\phi\cos\phi\right\rangle
\end{aligned}\]
(Note: The computation of the normal uses the parametrization, \(\vec R\),
but has nothing to do with the vector field, \(\vec F\).)
To check the orientation of the normal, we look at the \(z\) component of
the normal. If it is positive, then the normal points up or outward from
the sphere. In the upper hemisphere, \(\sin\phi\) and \(\cos\phi\) are
positive. So the \(z\) component of the normal is negative. This means the
normal is inwards, opposite of what we need it to be. So we reverse
\(\vec{N}\) and use that value for the remainder of our calculations.
\[
\text{Reverse:}\qquad\vec{N}
=\left\langle 4\sin^2\phi\cos\theta,4\sin^2\phi\sin\theta,4\sin\phi\cos\phi\right\rangle
\]
Next, we compute and simplify the dot product:
\[\begin{aligned}
\vec{F}\cdot\vec{N}
&=\left\langle 4\sin\phi\cos\phi\cos\theta,4\sin\phi\cos\phi\sin\theta,4\cos^2\phi\right\rangle \\
&\quad\cdot\left\langle 4\sin^2\phi\cos\theta,4\sin^2\phi\sin\theta,4\sin\phi\cos\phi\right\rangle \\
&=16\sin^3\phi\cos\phi\cos^2\theta+16\sin^3\phi\cos\phi\sin^2\theta+16\sin\phi\cos^3\phi \\
&=16\sin^3\phi\cos\phi(\cos^2\theta+\sin^2\theta)+16\sin\phi\cos^3\phi \\
&=16\sin\phi\cos\phi(\sin^2\phi+\cos^2\phi)
=16\sin\phi\cos\phi
\end{aligned}\]
So the integral is
\[\begin{aligned}
\iint_P \vec{F}\cdot\,d\vec{S}
&=\iint_P \vec{F}(\vec R(\theta,\phi))\cdot\vec{N}\,d\theta\,d\phi \\
&=\int_0^{\pi/6}\int_0^{2\pi} (16\sin\phi\cos\phi)\,d\theta\,d\phi \\
&=2\pi\left[8\sin^2\phi\dfrac{}{}\right]_0^{\pi/6}
=16\pi\sin^2\left(\dfrac{\pi}{6}\right)
=4\pi
\end{aligned}\]
When we parametrized the surface, we could have named it \(\vec R(\phi,\theta)\) with \(\theta\) and \(\phi\) reversed. Then the normal would have been \[ \vec{N}=\vec{e}_\phi\times\vec{e}_\theta =\left\langle 4\sin^2\phi\cos\theta,4\sin^2\phi\sin\theta,4\sin\phi\cos\phi\right\rangle \] which is properly oriented and does not need to be flipped. However, in practice, there is no easy way to know in advance which order to use. So use either order and reverse the normal if necessary.
Compute \(\displaystyle \iint_P \vec{F}\cdot\,d\vec{S}\) where \(\vec{F}=\left\langle xz^2,yz^2,-2z^3\right\rangle\) and the surface is the piece of the paraboloid \(z=\dfrac{x^2+y^2}{5}\) below \(z=5\) orientated with the normal pointing down and out from the paraboloid. The normal vector was found in a previous exercise.
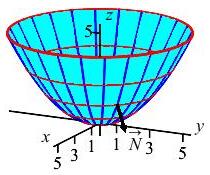
Don't forget to check the orientation of the normal and reverse it if necessary.
\(\displaystyle \iint_P \vec{F}\cdot\,d\vec{S}=3125\pi\)
From the previous exercise, the parametrization and normal vector are: \[\begin{aligned} \vec R(r,\theta) &=\left\langle r\cos\theta,r\sin\theta,\dfrac{r^2}{5}\right\rangle \\ \vec N &=\left\langle -\,\dfrac{2r^2}{5}\cos\theta,-\,\dfrac{2r^2}{5}\sin\theta,r\right\rangle \end{aligned}\] To check the orientation, notice \(N_z=r \gt 0\). So \(\vec N\) points up. Further, in the \(1^\text{st}\) quadrant, \(\sin\theta \gt 0\) and \(\cos\theta \gt 0\). So \(N_x \lt 0\) and \(N_y \lt 0\) and so \(\vec N\) points in. Since we need \(\vec N\) to point down and out, we reverse it: \[ \text{Reverse:}\qquad\vec{N} =\left\langle \dfrac{2r^2}{5}\cos\theta,\dfrac{2r^2}{5}\sin\theta,-r\right\rangle \] (Notice we reverse the entire vector.)
On the surface the vector field, \(\vec{F}=\left\langle xz^2,yz^2,-2z^3\right\rangle\), becomes: \[ \vec{F}(\vec R(r,\theta)) =\left\langle \dfrac{r^5}{25}\cos\theta,\dfrac{r^5}{25}\sin\theta, -\,\dfrac{2r^6}{125}\right\rangle \] The integrand is the dot product: \[\begin{aligned} \vec{F}\cdot\vec{N} &=\left\langle \dfrac{r^5}{25}\cos\theta,\dfrac{r^5}{25}\sin\theta,-\,\dfrac{2r^6}{125}\right\rangle \\ &\qquad\cdot \left\langle \dfrac{2r^2}{5}\cos\theta,\dfrac{2r^2}{5}\sin\theta,-r\right\rangle \\ &=\dfrac{2r^7}{125}\cos^2\theta+\dfrac{2r^7}{125}\sin^2\theta+\dfrac{2r^7}{125} =\dfrac{4r^7}{125} \end{aligned}\] So the integral is: \[\begin{aligned} \iint_P \vec{F}\cdot\,d\vec{S} &=\iint_P \vec{F}\cdot\vec{N}\,dr\,d\theta =\int_0^{2\pi}\int_0^5 \dfrac{4r^7}{125}\,dr\,d\theta \\ &=2\pi\left[\dfrac{r^8}{250}\right]_0^5 =3125\pi \end{aligned}\]
Notice that there is NO extra \(r\) in the integrand before the \(dr\,d\theta\) because \(r\) and \(\theta\) are parameters for a surface which just happen to have the same names as the cylindrical coordinates.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum